ABSOLEM.INFO | Формула Блэка-Шоулза.

\begin{equation} C(S,T) = SN(d_1) - K e^{-rT} N(d_2)) \\ \\ d_1 = \frac{\ln(\frac{S}{K}) + (r + \frac {\sigma^2}{2})T}{\sigma\sqrt{T}} \\ d_2 = \frac{\ln(\frac{S}{K}) + (r - \frac {\sigma^2}{2})T}{\sigma\sqrt{T}} = d_1 - \sigma\sqrt{T} \end{equation}

\(C(S,T)\) - премия европейского опциона колл;
\(S\) - курс спот актива;
\(T\) - время до истечения контракта (как часть года) (time to expiration);
\(K\) - цена исполнения опциона (цена страйк) (strike price/exercise price);
\(r\) - непрерывно начисляемая ставка без риска (risk-free interest rate);
\(\sigma \) - мгновенное стандартное отклонение актива волатильность (как часть года);
\(N(d_i)\) - функция нормального распределения.

Реализация на python

bsm_call_value.py

# -*- coding: utf-8 -*-
# файл bsm_call_value.py
def bsm_call_value(S0, K, T, r, sigma):
    """ Стоимость Европейского опциона call по модели BSM.
    Аналитическая формула.
    Параметры
    ==========
    S0 : float
        текущая цена актива
    K : float
        цена страйка
    T : float
        время до истечения (в частях года)
    r : float
        ставка без риска
    sigma : float
        фактор волатильности
    Возвращает
    =======
    value : float
        Текущая оценка стоимости Европейского call опциона
    """
    from math import log, sqrt, exp
    from scipy import stats
    S0 = float(S0)
    d1 = (log(S0 / K) + (r + 0.5 * sigma ** 2) * T) / (sigma * sqrt(T))
    d2 = (log(S0 / K) + (r - 0.5 * sigma ** 2) * T) / (sigma * sqrt(T))
    value = (S0 * stats.norm.cdf(d1, 0.0, 1.0) - K * exp(-r * T) * stats.norm.cdf(d2, 0.0, 1.0))
    return value

if __name__ == "__main__":
    S0 = 79790
    K = 80000
    T = 1.0/252*2
    r = 0.0
    sigma = 0.4
    print(bsm_call_value(S0, K, T, r, sigma))

Теперь попробуем найти волатильность, зная все параметры в том числе и цену опциона на бирже.

Дельта (Delta) \( \Delta \)

\( \Delta = \frac{\partial C}{\partial S} \) Дельта это скорость изменения цены опциона от изменения цены базового актива. \begin{equation} \text{Для опциона колл: } \Delta_{call} = N(d_1) \\ \text{Для опциона пут: } \Delta_{put} = -N(-d_1) = N(d_1) - 1 \end{equation}

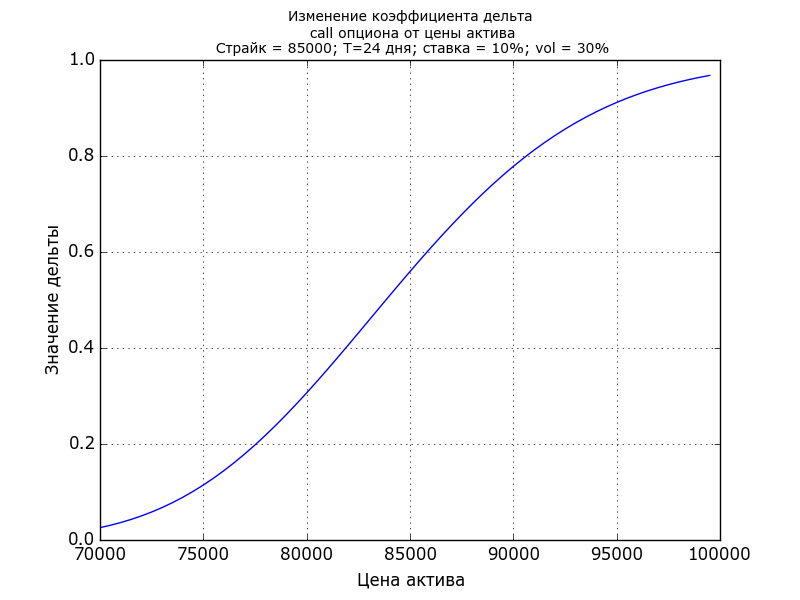
Построим график зависимости дельты от цены базового актива. Для этого зафиксируем страйк(K), времядо окончания контракта(T), безрисковую ставку(r) и волотильность(\(\sigma\)). Будем менять только цену базового актива. Полученный график представлен на рисунке 1.

Рис. 1

Python код с помощью которого построен график

Теперь построим график типичных зависимостей дельты от времени до конца контракта. Для этого зафиксируем три типичных страйка(K), в деньгах, на деньгах и вне денег. Также зафиксируем безрисковую ставку(r) и волотильность(\(\sigma\)). Будем менять только время до окончания опционного контракта. Полученный график представлен на рисунке 2.

Гамма (Gamma) \( \gamma \)

\[ \gamma = \frac{\partial^2 C}{\partial S^2} = \frac{N'(d1)}{S \sigma \sqrt{T}} \]

скорость изменения цены опциона от изменения Дельты (или ускорение от изменения цены базового актива)

Вега (Vega) \( \)

\[ Vega = \frac{\partial C}{\partial \sigma} = SN(d_1) \sqrt{T} \]

— описывает зависимость цены опциона от изменения волатильности базового актива. Вега отражает число пунктов изменения стоимости опциона на каждый процентный пункт (1%) изменения волатильности.

Тета (Theta) \( \theta \)

описывает снижение цены опциона в зависимости от времени до экспирации

\[ \theta = \frac{\partial C}{\partial T} \] \[ {для кола }\theta = - \frac{ CN(d_1) \sigma}{2\sqrt{T}} - rKe^{-rT}N(d_2) \] \[ {для пута }\theta = - \frac{ CN(d_1) \sigma}{2\sqrt{T}} + rKe^{-rT}N(-d_2) \]

Ро (Rho)

Хабр - Математика опционов или модель Блэка-Шоулза
Хабр - Лемма Ито
Хабр - Финансы в Excel+VBA. Калькулятор опционов по модели Блэка-Шоулза
macroption.com - Black-Scholes Formulas
investopedia.com - Black-Scholes Model: What It Is, How It Works, and Options Formula

Формула Блэка-Шоулза.Обновлено: март 2025.