Тест Дики-Фуллера(ADF) и тест Квятковского-Филлипса-Шмидта-Шина(KPSS)

Основные моменты

Стационарность означает, что статистические свойства временного ряда, т. е. среднее значение, дисперсия и ковариация, не меняются с течением времени. Многие статистические модели требуют, чтобы ряды были стационарными, чтобы делать эффективные и точные прогнозы.

Для проверки стационарности временного ряда будут использоваться два статистических теста — расширенный тест Дики-Фуллера («ADF») и тест Квятковского-Филлипса-Шмидта-Шина («KPSS»). Также попробуем преобразовать нестационарный временной ряд в стационарный ряд.

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import statsmodels.api as sm

Для примера будем использовать набор данных солнечных пятен. Он содержит ежегодные (1700-2008 гг.) данные о солнечных пятнах из Национального центра геофизических данных.

sunspots = sm.datasets.sunspots.load_pandas().data

Проведем предварительную подготовку данных. Будем использовать "YEAR" как индекс, а сам столбец "YEAR" удалим.

sunspots.index = pd.Index(sm.tsa.datetools.dates_from_range("1700", "2008"))
del sunspots["YEAR"]

Теперь постороим график

sunspots.plot(figsize=(12, 8))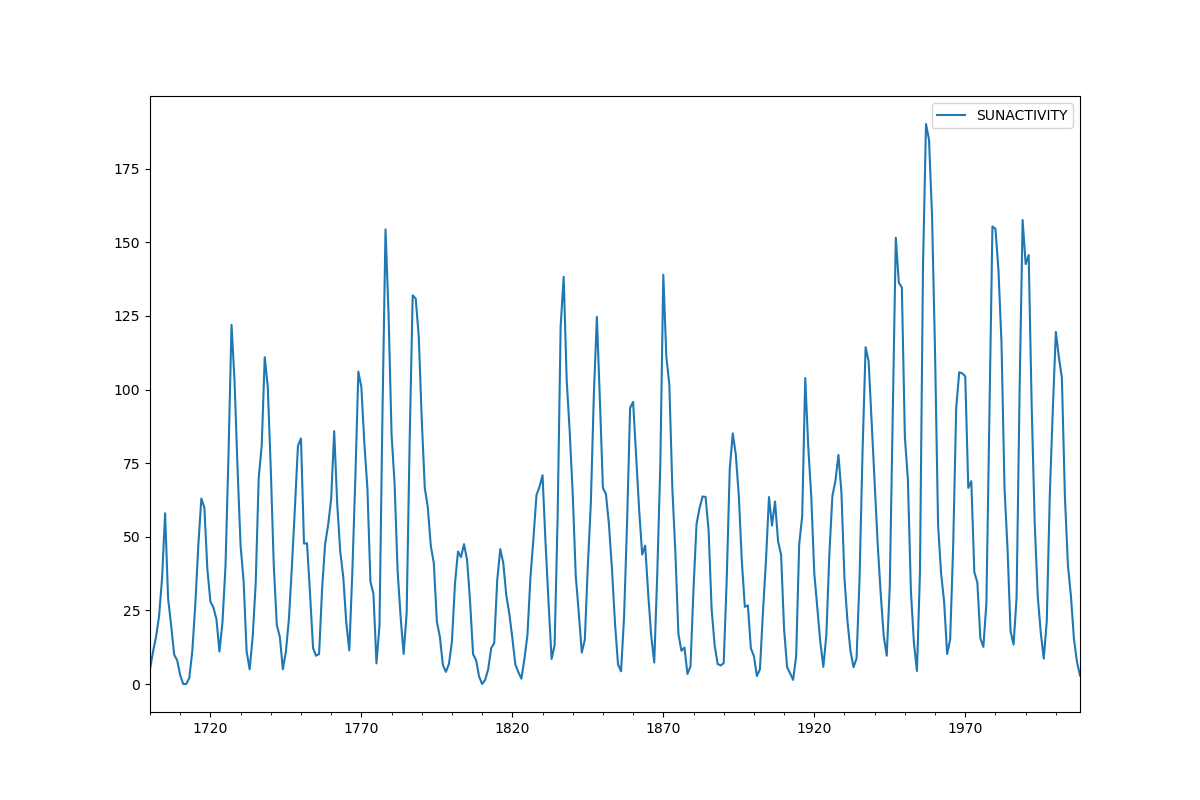

Тест ADF

Тест ADF используется для определения наличия единичного корня в ряду и, следовательно, помогает понять, является ли ряд стационарным или нет.

Если нулевую гипотезу не удалось отвергнуть, этот тест может свидетельствовать о нестационарности ряда.

Создадим функцию для проведения теста ADF на временном ряду.

from statsmodels.tsa.stattools import adfuller
 
 
def adf_test(timeseries):
    print("Results of Dickey-Fuller Test:")
    dftest = adfuller(timeseries, autolag="AIC")
    dfoutput = pd.Series(
        dftest[0:4],
        index=[
            "Test Statistic",
            "p-value",
            "#Lags Used",
            "Number of Observations Used",
        ],
    )
    for key, value in dftest[4].items():
        dfoutput["Critical Value (%s)" % key] = value
    print(dfoutput)

Тест KPSS

KPSS — еще один тест для проверки стационарности временного ряда. Нулевая и альтернативная гипотезы для теста KPSS противоположны таковым для теста ADF.

Нулевая гипотеза: процесс является стационарным по тренду.

Альтернативная гипотеза: ряд имеет единичный корень (ряд не является стационарным).

Напишем функцию для проведения теста KPSS на временном ряду.

from statsmodels.tsa.stattools import kpss
 
 
def kpss_test(timeseries):
    print("Results of KPSS Test:")
    kpsstest = kpss(timeseries, regression="c", nlags="auto")
    kpss_output = pd.Series(
        kpsstest[0:3], index=["Test Statistic", "p-value", "Lags Used"]
    )
    for key, value in kpsstest[3].items():
        kpss_output["Critical Value (%s)" % key] = value
    print(kpss_output)

Тест ADF дает следующие результаты - статистика теста, значение p и критическое значение при доверительных интервалах 1%, 5% и 10%.

Вызовем тест ADF.

adf_test(sunspots["SUNACTIVITY"])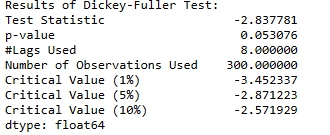

Основываясь на уровне значимости 0,05 и p-значении теста ADF, нулевую гипотезу нельзя отвергнуть. Следовательно, ряд нестационарен.

Вызовем тест KPSS.

kpss_test(sunspots["SUNACTIVITY"])

Основываясь на уровне значимости 0,05 и p-значении теста KPSS, есть основания отвергнуть нулевую гипотезу в пользу альтернативы. Следовательно, по тесту КПСС ряд является нестационарным.

Удаление тренда путем дифференцирования

Это один из самых простых методов устранения тренда временного ряда. Строится новый ряд, в котором значение на текущем временном шаге рассчитывается как разница между исходным наблюдением и наблюдением на предыдущем временном шаге.

Вычислим разность. Нарисуем график.

sunspots["SUNACTIVITY_diff"] = sunspots["SUNACTIVITY"] - sunspots["SUNACTIVITY"].shift(1)
diff = sunspots["SUNACTIVITY_diff"].dropna()
 
plt.figure(figsize=(12,8))
fig2 = plt.figure(2)
ax1 = fig2.add_subplot(111)
ax1.grid(True)
ax1.set_xlabel('Date')
ax1.set_ylabel('Difference')
plt.plot(diff, color='blue', label='Diff')
plt.legend(loc='best')
plt.title('Sun Activity Difference')
save("ADF_KPSS_pic_4")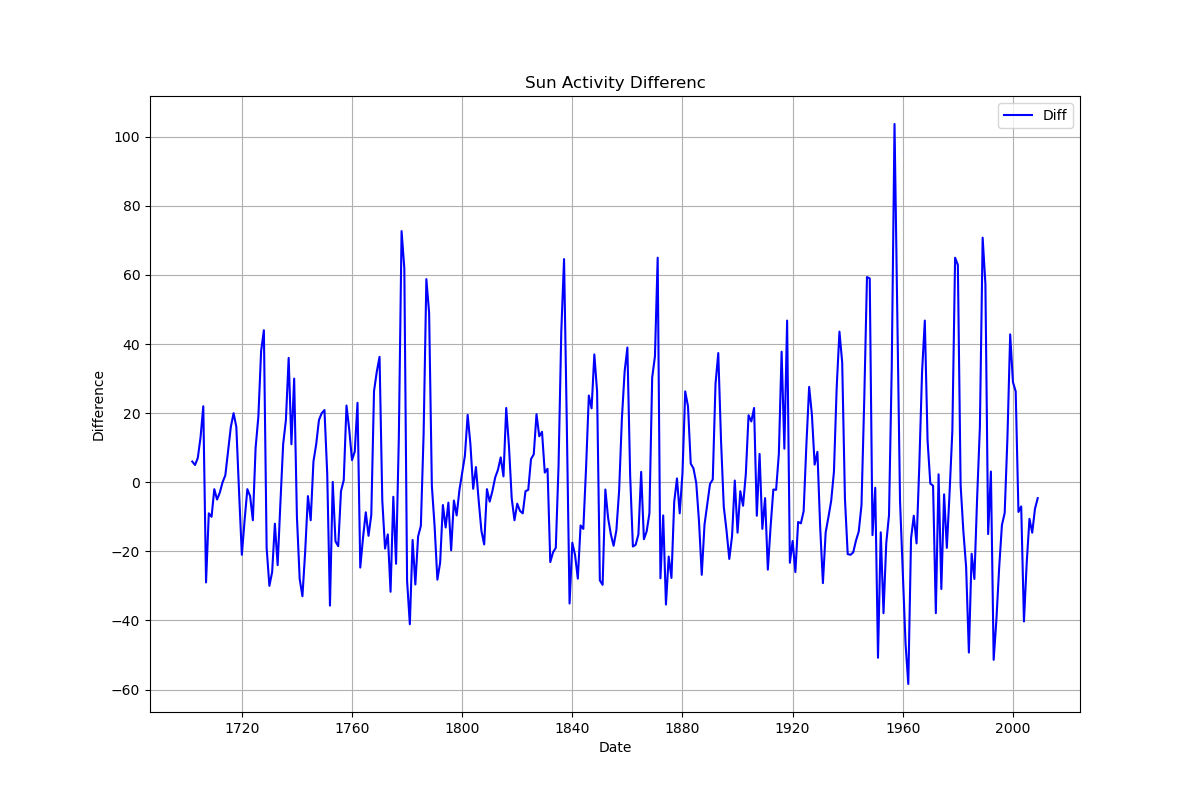

Проверим полученный ряд на стационарность, запустив тесты ADF и KPSS.

adf_test(diff)
kpss_test(diff)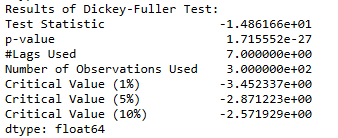

Основываясь на p-значении теста ADF, есть основания отвергнуть нулевую гипотезу в пользу альтернативы. Следовательно, ряд теперь строго стационарен.

Основываясь на p-значении теста KPSS, нулевую гипотезу нельзя отвергнуть. Следовательно, ряд является стационарным.

Полный текст примера:

ADF_example.py
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import statsmodels.api as sm
from statsmodels.tsa.stattools import adfuller
from statsmodels.tsa.stattools import kpss

# Утилита для записи графика в файл
import os
def save(name='', type='png'):
    pwd = os.getcwd()
    os.chdir('./pictures/')
    plt.savefig('%s.%s' % (name, type), format=type)
    os.chdir(pwd)

sunspots = sm.datasets.sunspots.load_pandas().data

sunspots.index = pd.Index(sm.tsa.datetools.dates_from_range("1700", "2008"))
del sunspots["YEAR"]

sunspots.plot(figsize=(12, 8))
save("ADF_KPSS_pic_1")


def kpss_test(timeseries):
    print("Results of KPSS Test:")
    kpsstest = kpss(timeseries, regression="c", nlags="auto")
    kpss_output = pd.Series(
        kpsstest[0:3], index=["Test Statistic", "p-value", "Lags Used"]
    )
    for key, value in kpsstest[3].items():
        kpss_output["Critical Value (%s)" % key] = value
    print(kpss_output)


def adf_test(timeseries):
    print("Results of Dickey-Fuller Test:")
    dftest = adfuller(timeseries, autolag="AIC")
    dfoutput = pd.Series(
        dftest[0:4],
        index=[
            "Test Statistic",
            "p-value",
            "#Lags Used",
            "Number of Observations Used",
        ],
    )
    for key, value in dftest[4].items():
        dfoutput["Critical Value (%s)" % key] = value
    print(dfoutput)
    
adf_test(sunspots["SUNACTIVITY"])
kpss_test(sunspots["SUNACTIVITY"])

sunspots["SUNACTIVITY_diff"] = sunspots["SUNACTIVITY"] - sunspots["SUNACTIVITY"].shift(1)
diff = sunspots["SUNACTIVITY_diff"].dropna()

plt.figure(figsize=(12,8))
fig2 = plt.figure(2)
ax1 = fig2.add_subplot(111)
ax1.grid(True)
ax1.set_xlabel('Date')
ax1.set_ylabel('Difference')
plt.plot(diff, color='blue', label='Diff')
plt.legend(loc='best')
plt.title('Sun Activity Difference')
save("ADF_KPSS_pic_4")

adf_test(diff)
kpss_test(diff)

Выводы

Используются два теста для проверки стационарности временного ряда, а именно тест ADF и тест KPSS. Удаление тренда осуществляется с помощью разности. Трендовый стационарный временной ряд преобразуется в строгий стационарный временной ряд. Необходимая модель прогнозирования теперь может быть применена к данным стационарного временного ряда.